Info

S&P 2024

Pennsylvania State University

代码地址：https://github.com/wanghangpsu/MM-BD

Abstract

后门攻击是针对深度神经网络分类器的一种重要对抗性威胁。当测试样本中嵌入后门pattern时，来自一个或多个源类别的样本会被（错误地）分类为攻击者指定的目标类别。本文关注文献中常见的训练后后门防御场景，即防御者在无法访问训练集的情况下，检测一个已训练分类器是否遭受后门攻击。许多训练后检测方法设计用于检测使用一种或几种特定后门嵌入函数（如补丁替换或加性攻击）的攻击。然而，当攻击者使用的后门嵌入函数（防御者未知）与防御者假定的后门嵌入函数不同时，这些检测方法可能失效。

相比之下，我们提出了一种训练后防御方法，可以检测具有任意类型后门嵌入的后门攻击，而无需对后门嵌入类型作任何假设。我们的检测器利用后门攻击对分类器在 softmax 层之前输出分布的影响，该影响独立于后门嵌入机制。对于每个类别，我们估计一个最大间隔统计量，并通过将无监督异常检测器应用于这些统计量来进行检测推断。因此，我们的检测器不需要任何合法的干净样本，并且能够高效检测具有任意源类别数量的后门攻击。

在四个数据集上，我们的检测器针对三种不同类型的后门模式以及多种攻击配置展示了优于多种最新方法的优势。此外，我们提出了一种新颖且通用的后门缓解方法，用于在检测后实施缓解。该缓解方法在首届 IEEE Trojan Removal Competition 中获得亚军。代码已在线公开。

Key Insight

本文的检测器基于后门攻击对分类器logits的影响，而这一影响独立于后门pattern类型。

Logits: logits 就是一个向量，下一步通常被投给 softmax/sigmoid 的向量。logits层通常产生$-\infin$到$+\infin$的值，而softmax层将其转换为0到1的值。

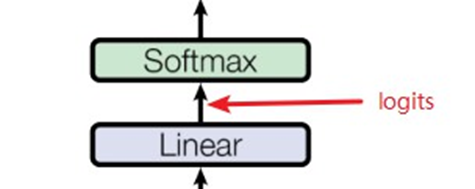
假设存在一个以目标类别 $t \in Y$为目标的后门攻击，并将与任何类别 $c \in Y$相关联的分类器的 logit 函数记为 $g_c : X → R$（在不失一般性的情况下假设 $X$是紧凑的）。对于所有 $c \in Y\setminus t$​，无论后门模式的类型如何，我们可能会观察到： $$ \max_{x\in \mathcal{X}}[g_t(x)-\max_{k\in \mathcal{Y}\setminus t}g_k(x)] \gg \max_{x\in \mathcal{X}}[g_c(x)-\max_{k\prime\in \mathcal{Y}\setminus c}g_k\prime(x)] \tag 1 $$ 即，对于真正的后门攻击目标类别（定义为上式左侧）的最大间隔统计量通常会远大于其他所有类别的最大间隔统计量（上式右侧）。

对于这一现象，作者给出的解释是：后门分类器中后门样本的内部特征由后门pattern（trigger）主导而不是源类的判别特征，trigger具有高度的重复性，而其他非目标类的区分特征通常表现出较高的变异性，例如，“鸟”类别中可能包含多种鸟类，甚至同一物体在不同视角、距离或光照条件下的不同表现形式。

为了实现较低的中毒率，trigger的高重复性不可避免，但是这也会引发过拟合，最终导致：

1. 提升目标类别logit
2. 抑制所有其他类别logit

由于上述“提高”和“抑制”效应，目标类别的logit与所有其他类别的logit之间会形成巨大的间隔。

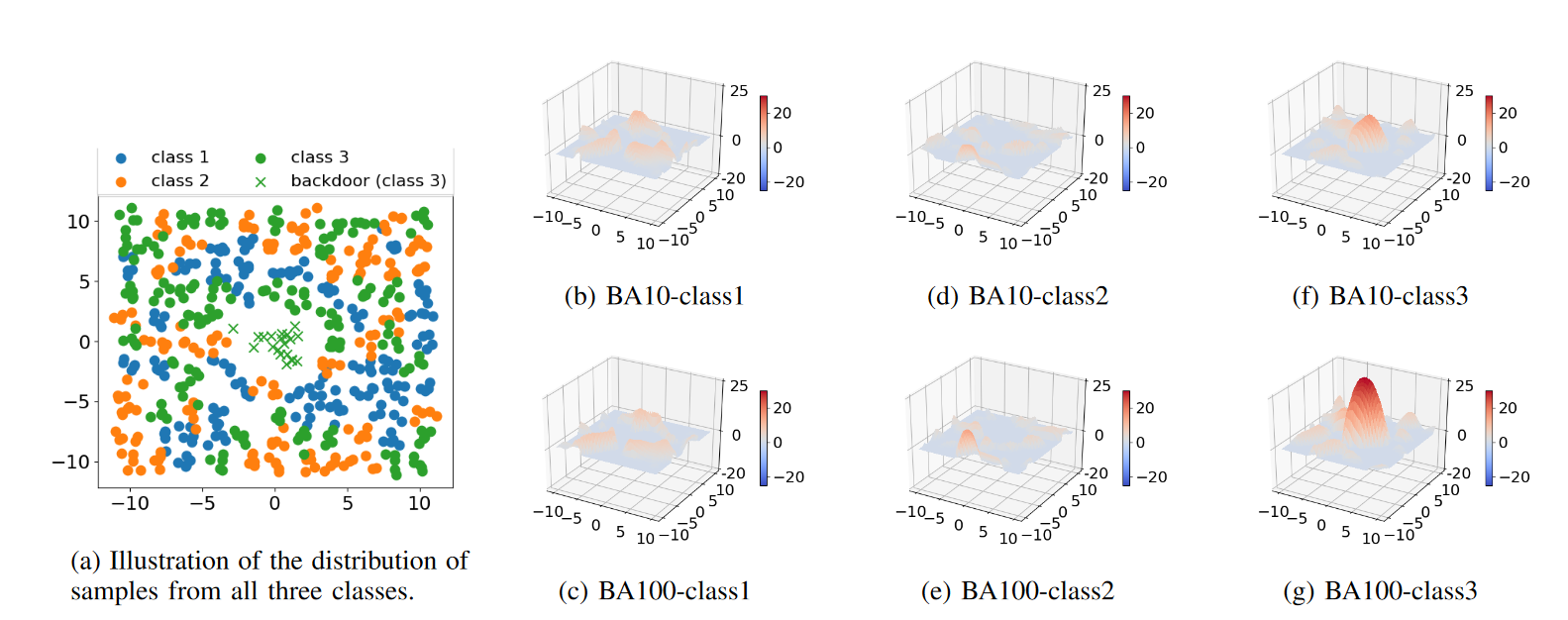
为了验证上面的推理，如下图所示，作者实现了一个toy可视化例子：首先根据高斯混合模型生成三个类别的二维输入，每个类别500个样本，然后以class3作为target label，分别插入了 10（BA-10）和 100（BA-100）个“后门样本”进行中毒。作者使用了具有三层隐藏层的多层感知机作为分类器模型，该模型在干净测试样本上的准确率几乎达到 91%，而在测试“后门样本”上的攻击成功率分别为 92% 和 99%。

对于每次后门攻击和每个类别，作者将一个类别的 logit 与其他两类中最大 logit 之间的差距作为输入空间的函数进行绘图。可以观察到，后门目标类别（图中f 和 g）的最大间隔在两种后门攻击下均异常大。此外，与 BA-10 相比，BA-100 的目标类别最大间隔异常现象更为明显。

Theoretical Analysis

与PEB类似，这里作者也进行了一番理论分析。

现在假设有一个简单的线性模型$g(·) : X → R^{|Y|}$，其中与类别$c \in Y$相关的输出由 logit $g_c$表示，其通过列向量点积计算得到：$g_c(x)=w_{c}^{\prime} x$​

其中：$w_c$ 代表与类别 $c$ 相关的权重向量，具有与输入 $x$ 相同的维度；模型对输入 $x$ 的类别决策 $c$ 对应于具有最大 logit $g_c(x)$的类别。假设在训练后，模型可以以超过 $\tau$ 的置信度正确分类所有训练样本，该置信度通过正确类别的间隔（即该类别的 logit 减去其他所有类别的最大 logit）评估： $$ g_y(x)-\max_{c\neq y}g_c(x)=w_{y}^{\prime}x-\max_{c\neq y}w_{c}^{\prime}x \ge \tau, \forall(x,y)\in X \times Y. \tag 2 $$ 假设后门模式 $v$ 被加性地嵌入到来自源类别 $s \neq t$的干净训练图像 $x_s$中，并将其重新标记为目标类别 $t$。公式 (2) 意味着： $$ g_t(x_s+v)-g_s(x_s+v)=w_{t}^{\prime}(x_s+v)-w_{s}^{\prime}(x_s+v) \ge \tau. \tag3 $$ 根据公式 (2) 中的置信间隔假设，对于干净的$x_s$，我们有： $$ w_{s}^{\prime}x_s-w_{t}^{\prime}x_s\ge\tau\tag4 $$ 将公式(3)和(4)相加，我们可以得到： $$ g_t(v)-g_s(v)=w_{t}^{\prime}v-w_{s}^{\prime}v\ge2\tau\tag5 $$ 即，后门目标类别的最大间隔下限至少为 $2\tau$，大于所有类别的合法样本的下限。

Treat Model

有些后门防御方法会在分类器的训练阶段部署，但这通常也是不可行的。在这里，我们考虑一个实际的训练后场景：在Model Zoo或者hugging face下载预训练模型的下游用户，只能检测分类器是否已受到攻击，而无法访问分类器的训练集，用户也无法访问任何未受攻击的分类器以供参考。

Dection

本文提出的后门检测方法大致分类两步，首先估计出每个类的最大间隔统计量，然后根据得到的最大间隔统计量，利用统计学的方法，判断最大间隔统计量是否存在异常，如有异常说明存在后门攻击。

Estimation Step

下面的内容修改自ChatGPT

对每个类别 $c \in Y$​，通过最大化“最大间隔统计量”来估计每个类别的异常行为。这个统计量反映了一个类别的 logit 与其他类别中最大 logit 之间的差距。公式如下： $$ \max_{x\in X}[g_c(x)-\max_{k\in Y\setminus c}g_k(x)] $$ 其中：

• $g_c(x)$：输入 $x$ 在类别 $c$ 下的 logit。
• $Y \setminus c$：所有类别中排除当前类别 $c$​ 的集合。
• $X$：输入空间（例如，对于彩色图像，$X = [0, 1]^{H \times W \times C}$，其中 $H$、$W$ 和 $C$​ 分别表示图像的高度、宽度和通道数）。

方法：

用**梯度上升法（Gradient Ascent）**来解决该优化问题：

• 梯度上升法通过调整输入 $x$ 来逐步逼近目标值，使得当前类别的最大边界统计量最大化。
• 为了保证优化过程在定义域内有效，我们对 $x$ 进行投影（Projection），确保其始终位于 $X$​ 内。

为什么梯度上升法可行？

• $X$是一个闭合凸集，logit 函数在 $X$上是连续的，因此是有界且满足 Lipschitz 条件（即函数在某些局部区域内的梯度是有限的）。

• 根据 Convex Optimization: Algorithms and Complexity 的定理 3.2，即使从随机初始化的点出发，通过梯度上升并投影回 $X$​ ，也可以保证收敛到局部最优解。

多次随机初始化：

• 为了避免局部最优解偏离全局最优，我们通常从 $X$​ 中进行多次随机初始化（例如，对图像来说，将像素值在 [0,1] 区间内随机初始化），然后选择最优解中最大的局部解。

与基于逆向工程的防御方法对比：

• 基于逆向工程的方法通常需要假设后门触发器的类型，并依赖干净样本来估计后门模式。这种方法在样本大多数来自非源类时效果会较差。
• 而本方法无需假设任何后门触发器的嵌入类型，也不需要领域中的干净样本，从而更具鲁棒性。

Inference Step

作者使用无监督的异常检测方法，判断最大间隔统计量是否存在异常值，从而检测后门攻击，具体步骤如下：

1. 定义最大间隔统计量

   对每个类别$c\in Y$，估计的最大间隔统计量用$r_c$表示。找到所有类别中最大的统计量： $$ r_{\text{max}}=\max_{c\in Y}r_c $$ 通常情况下，$r_{\text{max}}$对应于潜在的后门target类。

2. 假设检验

   假设无攻击的情况下，这些统计量（除了 $r_{\text{max}}$）服从某种原假设分布 $H_0$。我们在实验中选择单尾密度分布（例如，Gamma 分布）来建模$H_0$，因为理论上和经验上最大边界是严格为正的。

3. 计算p值

   为评估$r_{\text{max}}$在$H_0$下的异常程度，使用次序统计量计算p值： $$ pv = 1 - H_0(r_\text{max})^{K-1} $$ 其中： $K=|Y|$表示类别的总数，$H_0(r_\text{max})$表示最大间隔统计量$r_{\text{max}}$在$H_0$下的累积分布函数（CDF）。

4. 检测决策

   设定显著性水平$\theta$（例如经典值$\theta=0.05$）。如果$pv<\theta$，则以置信度$1-\theta$检测出后门攻击。

5. 推断目标类别

   一旦检测到后门攻击，将$r_{\text{max}}$所对应的类别推断为后门目标类别。

Mitigation

后门攻击利用了某些“异常激活”的神经元，使得模型对携带特定触发器的样本给出错误预测。我们需要找到一种方法来：抑制这些异常激活，从而降低后门攻击的成功率；但同时保持模型在正常样本上的性能。

文中提出的方法的核心思想是：对模型中每一层的每个神经元设置一个上限值，即限制它们的激活值不能超过这个上限。这可以防止后门攻击利用某些神经元过度激活，但同时我们也希望这个限制不会影响模型在正常样本上的性能。

Upper Bound

如何为每一个神经元都设置一个上限呢？我们知道，神经网络的输出是通过逐层计算得到的。假设模型有 LLL 层神经网络，输入数据为 xxx，我们可以表示每一层的激活输出：$\sigma_l(x)$为第$l$层的神经元激活值。

模型的预测结果(logit值)可以写成： $$ g_c(x)=w_c^T(\sigma_L\circ \sigma_{L-1}\circ\cdots\circ\sigma_1(x))+b_c $$ 这里$w_c$ 和 $b_c$ 是与类别 $c$​ 相关的权重和偏置。

于是，对每一层的神经元激活值，我们引入一个上限 $z_l$​，并定义一个新的激活函数： $$ \overline\sigma_l(x;z_l)=min{\sigma_l(x),z_l} $$ 这表示每个神经元的激活值不能超过$z_l$。

于是新的模型logit变成： $$ {g}{c}(x ; Z)=w{c}^{T}\left(\bar{\sigma}{L} \circ \bar{\sigma}{L-1} \circ \cdots \circ \bar{\sigma}{2}\left(\sigma{1}(x) ; z_{2}\right) \cdots ; z_{L}\right)+b_{c} $$ 这里$Z={z_2,z_3,\dots,z_L}$是所有层的上限值集合。

Optimization

为了保证缓解后的模型仍然可以在干净样本上正常工作，我们需要优化这些上限值$Z$。

数学上，这可以写成一个优化问题：： $$ \min_{Z = {z_2, \dots, z_L}} \sum_{l=2}^L ||z_l||2 $$ 即最小化所有上限值的二范数（尽可能小的上限值），同时满足以下约束： $$ \frac{1}{|D|} \sum{(x, y) \in D} 1[y = \arg \max_{c \in Y} \bar{g}_c(x; Z)] \geq \pi $$ 意思是：模型在干净样本 $D$ 上的分类准确率必须高于某个阈值 $\pi$。

由于直接优化上述约束问题可能比较困难，作者提出通过拉格朗日乘子法来解决问题： $$ L(Z, \lambda; D) = \frac{1}{|D| \times |Y|} \sum_{(x, y) \in D} \sum_{c \in Y} [\bar{g}c(x; Z) - g_c(x)]^2 + \lambda \sum{l=2}^L ||z_l||_2 $$ –TBD–